El efecto Dzhanibekov

Hoy algo del campo de la física para el curioso: El Efecto Dzhanibekov, también conocido como el teorema de la raqueta de tenis, explica la inestabilidad de los cuerpos en rotación con tres momentos de inercia diferentes. El momento de inercia indica la resistencia de un cuerpo a cambios en su movimiento de rotación. Depende del eje de rotación particular y de la geometría. Comprender la dinámica de los sistemas hamiltonianos clásicos sigue siendo un objetivo crucial con una multitud de aplicaciones que van mucho más allá de su descripción matemática. En el caso de sistemas integrables con pocos grados de libertad, un enfoque eficiente se basa en un análisis geométrico para caracterizar las propiedades dinámicas del sistema mecánico. Estos fenómenos geométricos suelen ser el origen de la robustez de ciertos efectos que pueden observarse experimentalmente. uno de ellos es el llamado. Efecto Dzhanibekov o también llamado efecto raqueta de tenis.

Efecto Janibekov en la ingravidez de la ISS

Una excelente y detallada derivación teórica del fenómeno se puede encontrar aquí (https://arxiv.org/pdf/1606.08237.pdf). Se trata aquí de uno que es un poco más rudo, pero que sin embargo explica el fenómeno. Desafortunadamente, aquí es necesario algún conocimiento previo de la dinámica de los cuerpos rígidos:

Considere una matriz de inercia (diagonalizada) con momentos de inercia I1 e I2 e I3 tales que I1 es el más pequeño e I3 es el más grande. Ahora considere el movimiento alrededor del eje del momento de inercia principal I3. El vector de velocidad angular es:

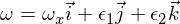
donde los épsilons son pequeñas perturbaciones en los otros dos ejes principales. Si ahora inserta esto en las ecuaciones de Euler, obtiene:

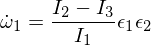
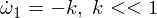
Ahora diferenciamos la segunda ecuación de Euler:

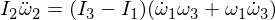
La sustitución de omega 1 y omega 3 en nuestra expresión, y dado que multiplicar los épsilones los hace lo suficientemente pequeños como para ignorarlos,

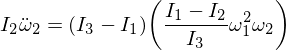
Esto nos da una ecuación diferencial para Omega 2 de la forma:

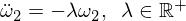
La solución básica es:

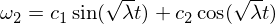
Por lo tanto, sabemos que el desorden rotacional en el eje omega-1 es estable y hace movimientos periódicos, o en la terminología del movimiento rígido del cuerpo, que hace una precesión. El trastorno de omega 3 sigue un argumento similar al anterior, y lo dejaré como un ejercicio para que lo resuelva. Para el eje intermedio tenemos:

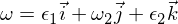
Insertado en las ecuaciones de Euler:

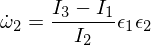
Al diferenciar la tercera ecuación de Euler se obtiene:

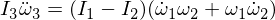
Reemplacemos nuestras expresiones derivadas:

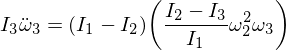
Ahora reorganice y obtenga la siguiente ecuación diferencial:

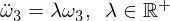
Observe que el coeficiente ahora es positivo, lo que, por lo tanto, conduce a soluciones exponenciales:

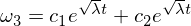
¡Esta solución muestra que el omega 3 es inestable a lo largo del eje intermedio con una alteración del omega 2!

¿Qué significa esto?

Ahora podemos combinar todo lo que hemos derivado y aprendido para comprender el teorema. En términos simples, si se altera la rotación a lo largo del eje intermedio, se obtiene una ecuación diferencial con soluciones exponenciales. Esto conduce a un movimiento inestable, en contraste con el movimiento preciso observado en los otros dos ejes. Este resultado es bastante sorprendente. No existe un apoyo intuitivo para tal teorema, ya que no podemos imaginar por qué el momento de inercia intermedio daría como resultado una rotación inestable. Parece que es de naturaleza puramente matemática.